HDE Lecture Notes
J. R. Carey		Life Tables and Mortality
Winter, 1999		Set #2

The Life Table

Death rate is a primary vital statistic along with birth and marriage. It is important because it: (1)is a barameter of current health in a population; (2)identifies trends in health and mortality by indicating at what age most deaths are occuring and the causes of death; and (3)provides a baseline for prediction of trends for the future which can be used for life insurance, medicare, social security and business. The main analytical tool for examining mortality and longevity in populations is the life table. The life table is a product of actuarial science (life insurance). The first life table was developed in 1662 in England by John Graunt when he published "The Bills of Mortality". This was useful as a concept (ordering mortality data) but there was very unreliable mortality data available at that time. It was not until 1900 that reliable mortality data became available.

Knowledge of some background terms and concepts will be useful for understanding of life table techniques.

Some of the life table parameters express mortality or survival as a probability given as the number of individuals which experience an event (like death or marriage) divided by the number that are at risk of experiencing that event. For example, if 2 people died out of a pool of 100 people who were subjected to a toxic substance we would say that the probability of dying given this exposure is 0.02 or 2%. This is what is referred to as an a posteriori probability since the death rate is after the fact; that is, it is not possible to predict the death rate or probability without first conducting the "experiment". This is distinct from an a priori probability which expresses a probability before the fact (of the experiment). For example, we can easily estimate the probability of a coin landing heads (0.50 or 50%) without first flipping the coin 100 times. Mortality rates are a posteriori probabilities; that is, the number of deaths relative to the number of persons at risk must be determined from retrospective estimates.

A life table is a detailed description of the age-specific mortality, survival and expectation of life of a population. Life tables help to answer questions such as: What is the life expectancy of the average newborn? How many years remains for the average 75 year old woman in the U.S. Over what age groups do most deaths occur? What is the probability of dying in the next year given that you are age 18? What is this probability at age 80? What fraction of all 1990 newborn will live to age 85? What proportion will live from age 50 to age 90?

There are two general forms of the life table. The first is the cohort life table which provides a longitudinal perspective in that it includes the mortality experience of a particular cohort from the moment of birth through consecutive ages until none remains in the original cohort. The second basic form is the current life table which is cross-sectional. This table assumes a hypothetical cohort subject throughout its lifetime to the age-specific mortality rates prevailing for the actual population over a specified period and are used to construct a synthetic cohort. Both forms of the life table may be either single decrement or multiple decrement. The first of these lumps all forms of death into one and the second disaggregates death by cause.

Life Table Functions

The life table is organized in seven columns starting with an age x column from 0 through the age of the oldest person ever to live around 120 years.

Table 1. Hypothetical life table showing the main functions.

Age
x
(1)		 Living at
Age x
Nx
(2)		 Cohort
survival
to age x
lx
(3)		 Survival
from
x to x+1
px
(4)		 Mortality
in interval
x to x+1
qx
(5)		 Deaths
in interval
x to x+1
dx
(6)		 Expectation
of life
at age x
ex
(7)
0 100,000 1.000 .900 .100 .100 2.40
1 90,000 .900 .556 .444 .400 1.61
2 50,000 .500 .800 .200 .100 1.50
3 40,000 .400 .250 .750 .300 .75
4 10,000 .100 .000 1.000 .100 .50
5 0 -- -- -- -- --

lx= proportion of all newborn surviving to age x
px = proportion of individuals alive at age x that survive to x+1
qx = proportion of individuals alive at age x that die prior to x+1
dx = proportion of all newborn that die in the interval x to x+1
ex = expected lifetime remaining to the average individual age x

Column 1. The first column of a life table contains all age classes denoted x and ranges from 0 (newborn) through the oldest possible age, .

Column 2. This column gives the number of the original cohort alive at age x and is denoted Nx. The initial number is typically 100,000 and is known as the life table radix.

Column 3. This column contains cohort survival, lx, defined as the fraction of the original cohort surviving to age x. The general formula is given as

For example:

= 1.0000 = 0.4000

Survival

Column 4. The parameter defined in this column is known as period survival, px, defined as the fraction of individuals alive at age x that survive to age x+1. The general formula is given as

For example the period survival rates for ages x=0 and x=3 from Table 1 are

= 0.90 = 0.25

Thus the probability of surviving from age 0 to 1 is 0.90 and from age 3 to 4 is 0.25.

Column 5. This column contains the compliment of period survival and is known as period mortality, qx, defined as the fraction of individuals alive at age x that die prior to age x+1. The general formula is

or

qx = 1 - px

For example, the period mortality rates for ages x=0 and x=3 from Table 1 are
q0 = 1 - p0 q3 = 1 - p3
= 1.00 - 0.90 = 1.00 - 0.25
= 0.10 = 0.75
Thus the fraction of individuals that are alive at age 0 but die prior to age 1 is 0.10 and the fraction that are alive at age 3 but die prior to age 4 is 0.75.

Age-Specific Mortality

Column 6. The parameter contained in this column is the fraction of the original cohort that dies in the interval x to x+1 and is denoted dx. It is the frequency distribution of deaths and is given by the formula

dx = lx - lx+1

For example, the value of dx for ages x=0 and x=3 from Table 1 are

d0 = l0 - l1 d3 = l3 - l4
= 1.00 - 0.90 = 0.14 - 0.10
= .10 = .30

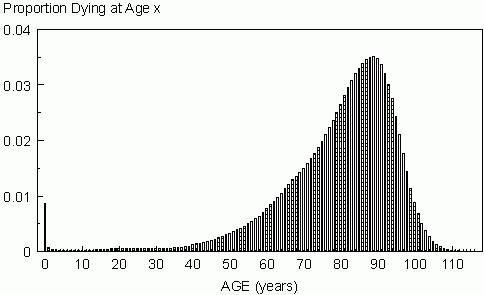
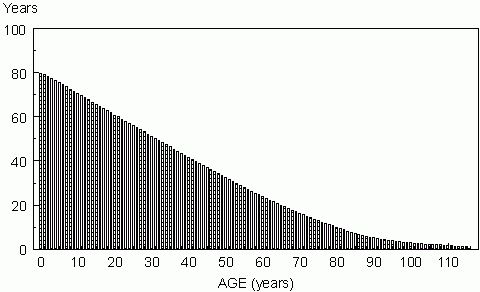
Thus the fraction of the original cohort that dies in the interval 0 to 1 is 0.10 and the fraction that dies in the interval 3 to 4 is 0.30.

Frequency Distribution of Deaths

Column 7. This column contains the parameter expectation of life, ex, which is defined as the average number of years (days, weeks) remaining to an individual age x. The general formula is given by

For example, the value of dx for ages x =0 and x=3 from Table 1 are

= 2.40 = 0.75

Thus the expectation of life at birth, e0, is 2.4 and at age 3, e3, is 0.75.

Expectation of Life

Current Life Table

A current life table is based on the concept of a synthetic cohort in which the probabilities of dying from one age class to the next are based on the death rates of each of the 115+ cohorts living at any one time. The idea is based on the notion that the probability of surviving to say, age 5, is the probability (or fraction) or newborn individuals living to age 1 times the probability of age 1 individuals living to age 2 times the probability of age 2 individuals living to age 3 and so forth. Thus the general form for reconstructing a survival curve and, in turn, all other life table parameters from period survival (or period mortality) data is

lx = p0 × p1 × p2 × ... × px-1

For example, suppose we wish to construct a survival curve from the death rates prevailing from 1990 to 1991 as given in Table 2. The probability of an individual age 0 in 1990 surviving to age 1 in 1991 is

= 0.8364

Table 2. Number of persons in hypothetical census by age class and year.
Age
Year 0 1 2 3
1990 110,000 121,000 110,000
1991 92,000 100,000 101,000

Similarly for the probabilities for individuals surviving from age 1 to 2 and age 2 to 3

= 0.8264

= .09182

Thus a synthetic survival schedule can be constructed by multiplying progressively as

Age px lx Nx
0 0.8364 1.0000 100,000
1 0.8264 0.8364 83,640
2 0.9182 0.6912 69,120
3 0.6347 63,470

Thus out of 100,000 individuals age 0, 83,640 will survive to age 1. This is based on the 1990 to 1991 probability of survival from 0 to 1 years. Out of these 83,640 individuals alive at age 1, 0.8264 of these or 69,120 will survive to age 2. Out of these 69,120 individuals alive at age 2, 0.9182 or 63,470 will survive to age 3. In other words, the fraction that survive to age x equals the product of the fractions (or probabilities) that survive through each of the previous age classes.

Both the cohort life table and the current life table are based on assumptions that are violated in reality. The cohort life table is based on the mortality experience of the same group of individuals from birth through the age when the last individuals dies. Thus if we were to use only cohort life tables to characterize longevity in the U.S., then the only life tables available would be for cohorts in which all individuals have died, the earliest of which would be individuals born around 1880. First, there is the problem of obtaining accurate records of mortality rates over a century ago and second, there is the problem that mortality rates in 1880 were much higher at all age classes than are current mortality rates. Third, the centenarians of today when through much more difficult times than will future centenarians. Thus their mortality rates may be much higher than will be the future centenarians.

But the current life table also has problems (though many fewer). First, the current life table is cross sectional. Thus every cohort will have a different history. And it is well known that the experiences at younger ages has an impact on mortality rates at older ages. Take for example, two cohorts aged 10 and 50. Suppose the cohort age 50 was severely malnourished when they were age 10 years assumes that when the 10 year old cohort attains age 50 they will experience the same mortality rate as the 50-year old cohort does this year. Clearly they have different experiences that will have a major bearing on their mortality rates at older ages.

Table 1. Life table for 1970 birth cohort subjected to mortality rates of 1990 U.S. females.

Year Age Number
Remaining
Alive		 Survival
to
age x
lx		 Survival
from x to
x+1
px		 Mortality
from x to
x+1
qx		 Fraction dying
x to
x+1
dx		 Number
dying x to
x+1
Dx		 Expecta-
tion of
life
ex
1970 0 3731000 1.0000 .9914 .0086 .0086 31975 79.9
1971 1 3699025 .9914 .9993 .0007 .0007 2537 79/5
1972 2 3696488 .9908 .9996 .0004 .0004 1567 78.6
1973 3 3694921 .9903 .9997 .0003 .0003 1194 77.6
1974 4 3693727 .9900 .9997 .0003 .0002 933 76.7
1975 5 3692795 .9898 .9998 .0002 .0002 821 75.7
1976 6 3691974 .9895 .9998 .0002 .0002 746 74.7
1977 7 3691228 .9893 .9998 .0002 .0002 709 73.7
1978 8 3690519 .9892 .9998 .0002 .0002 634 72.7
1979 9 3689884 .9890 .9998 .0002 .0002 597 71.7
1980 10 3689287 .9888 .9998 .0002 .0002 597 70.7
1981 11 3688690 .9887 .9998 .0002 .0001 560 69.8
1982 12 3688131 .9885 .9998 .0002 .0002 672 68.8
1983 13 3687459 .9883 .9998 .0002 .0002 784 67.8
1984 14 3686676 .9881 .9997 .0003 .0003 1007 66.8
1985 15 3685668 .9879 .9997 .0003 .0003 1269 65.8
1986 16 3684400 .9875 .9996 .0004 .0004 1455 64.8
1987 17 3682945 .9871 .9996 .0004 .0004 1642 63.9
1988 18 3681303 .9867 .9995 .0005 .0005 1716 62.9
1989 19 3679587 .9862 .9995 .0005 .0005 1791 61.9
1990 20 3677796 .9857 .9995 .0005 .0005 1791 60.9
1991 21 3676005 .9853 .9995 .0005 .0005 1866 60.0
1992 22 3674140 .9848 .9995 .0005 .0005 1903 59.0
1993 23 3672237 .9843 .9995 .0005 .0005 1940 58.0
1994 24 3670297 .9837 .9995 .0005 .0005 1977 57.1
1995 25 3668319 .9832 .9994 .0006 .0006 2089 56.1
1996 26 3666230 .9826 .9994 .0006 .0006 2127 55.1
1997 27 3664103 .9821 .9994 .0006 .0006 2127 54.2
1998 28 3661977 .9815 .9994 .0006 .0006 2164 53.2
1999 29 3659813 .9809 .9994 .0006 .0006 2127 52.2
2000 30 3657686 .9804 .9994 .0006 .0006 2164 51.2
2001 31 3655522 .9798 .9994 .0006 .0006 2164 50.3
2002 32 3653358 .9792 .9994 .0006 .0006 2239 49.3
2003 33 3651119 .9786 .9994 .0006 .0006 2276 48.3
2004 34 3648843 .9780 .9993 .0007 .0006 2388 47.4
2005 35 3646456 .9773 .9993 .0007 .0007 2500 46.4
2006 36 3643956 .9767 .9993 .0007 .0007 2649 45.4
2007 37 3641307 .9760 .9992 .0008 .0008 2947 44.5
2008 38 3638359 .9752 .9991 .0009 .0009 3395 43.5
2009 39 3634964 .9743 .9989 .0011 .0010 3880 42.5
2010 40 3631084 .9732 .9988 .0012 .0012 4515 41.6
2011 41 3626569 .9720 .9986 .0014 .0014 5149 40.6
2012 42 3621421 .9706 .9984 .0016 .0015 5783 39.7
2013 43 3615637 .9691 .9982 .0018 .0017 6380 38.8
2014 44 3609257 .9674 .9981 .0019 .0019 6977 37.8
2015 45 3602281 .9655 .9979 .0021 .0020 7611 36.9
2016 46 3594669 .9635 .9977 .0023 .0022 8320 36.0
2017 47 3586349 .9612 .9975 .0025 .0025 9141 35.1
2018 48 3577208 .9588 .9972 .0028 .0027 10074 34.1
2019 49 3567134 .9561 .9969 .0031 .0030 11044 33.2
2020 50 3556091 .9531 .9966 .0034 .0033 12200 32.3
2021 51 3543890 .9499 .9962 .0038 .0036 13357 31.4
2022 52 3530533 .9463 .9959 .0041 .0039 14588 30.6
2023 53 3515945 .9424 .9955 .0045 .0042 15857 29.7
2024 54 3500088 .9381 .9951 .0049 .0046 17200 28.8
2025 55 3482889 .9335 .9947 .0053 .0050 18580 28.0
2026 56 3464308 .9285 .9942 .0058 .0054 20147 27.1
2027 57 3444161 .9231 .9936 .0064 .0059 21938 26.3
2028 58 3422222 .9172 .9930 .0070 .0064 24028 25.4
2029 59 3398195 .9108 .9922 .0078 .0071 26341 24.6
2030 60 3371854 .9037 .9915 .0085 .0077 28766 23.8
2031 61 3343088 .8960 .9906 .0094 .0084 31340 23.0
2032 62 3311748 .8876 .9897 .0103 .0091 33952 22.2
2033 63 3277795 .8785 .9888 .0112 .0098 36601 21.4
2034 64 3241194 .8687 .9879 .0121 .0105 39325 20.7
2035 65 3201870 .8582 .9868 .0132 .0113 42235 19.9
2036 66 3159635 .8469 .9857 .0143 .0121 45257 19.2
2037 67 3114378 .8347 .9845 .0155 .0129 48167 18.4
2038 68 3066210 .8218 .9835 .0165 .0136 50742 17.7
2039 69 3015469 .8082 .9823 .0177 .0143 53316 17.0
2040 70 2962153 .7939 .9811 .0189 .0150 56114 16.3
2041 71 2906039 .7789 .9796 .0204 .0159 59286 15.6
2042 72 2846753 .7630 .9780 .0220 .0168 62569 14.9
2043 73 2784184 .7462 .9763 .0237 .0177 66039 14.3
2044 74 2718145 .7285 .9744 .0256 .0187 69695 13.6
2045 75 2648450 .7099 .9721 .0279 .0198 73799 12.9
2046 76 2574651 .6901 .9696 .0304 .0210 78351 12.3
2047 77 2496300 .6691 .9667 .0333 .0223 83127 11.7
2048 78 2413173 .6468 .9635 .0365 .0236 88126 11.1
2049 79 2325047 .6232 .9599 .0401 .0250 93312 10.5
2050 80 2231735 .5982 .9557 .0443 .0265 98909 9.9
2051 81 2132826 .5717 .9509 .0491 .0281 104692 9.3
2052 82 2028134 .5436 .9457 .0543 .0295 110139 8.8
2053 83 1917995 .5141 .9401 .0599 .0308 114915 8.2
2054 84 1803080 .4833 .9339 .0661 .0320 119205 7.7
2055 85 1683875 .4513 .9269 .0731 .0330 123048 7.2
2056 86 1560827 .4183 .9190 .0810 .0339 126444 6.8
2057 87 1434383 .3845 .9100 .0900 .0346 129130 6.3
2058 88 1305253 .3498 .8998 .1002 .0350 130734 5.9
2059 89 1174519 .3148 .8885 .1115 .0351 130921 5.5
2060 90 1043598 .2797 .8761 .1239 .0347 129279 5.1
2061 91 914319 .2451 .8626 .1374 .0337 125623 4.8
2062 92 788696 .2114 .8481 .1519 .0321 119840 4.5
2063 93 668856 .1793 .8324 .1676 .0300 112079 4.2
2064 94 556777 .1492 .8159 .1841 .0275 102528 3.9
2065 95 454249 .1218 .7994 .2006 .0244 91111 3.7
2066 96 363138 .0973 .7835 .2165 .0211 78612 3.5
2067 97 284526 .0763 .7686 .2314 .0177 65852 3.3
2068 98 218674 .0586 .7546 .2454 .0144 53652 3.1
2069 99 165022 .0442 .7423 .2577 .0114 42533 3.0
2070 100 122489 .0328 .7295 .2705 .0089 33131 2.8
2071 101 89357 .0240 .7161 .2839 .0068 25371 2.7
2072 102 63987 .0172 .7015 .2985 .0051 19103 2.6
2073 103 44884 .0120 .6874 .3126 .0038 14029 2.4
2074 104 30855 .0083 .6711 .3289 .0027 10148 2.3
2075 105 20707 .0056 .6541 .3459 .0019 7164 2.2
2076 106 13544 .0036 .6391 .3609 .0013 4888 2.1
2077 107 8656 .0023 .6164 .3836 .0009 3321 2.0
2078 108 5335 .0014 .6014 .3986 .0006 2127 1.9
2079 109 3209 .0009 .5814 .4186 .0004 1343 1.8
2080 110 1866 .0005 .5800 .4200 .0002 784 1.7
2081 111 1082 .0003 .5517 .4483 .0001 485 1.6
2082 112 597 .0002 .5000 .5000 .0001 298 1.4
2083 113 298 .0001 .5000 .5000 .0000 149 1.4
2084 114 149 .0000 .5000 .5000 .0000 75 1.3
2085 115 75 .0000 .5000 .5000 .0000 37 1.0
2086 116 37 .0000 .0000 1.0000 .0000 37 0.5

Importance of Mortality

The life table provides five different expressions or functions which describe the mortality and survival experience of a cohort. Because each of the functions can be independently derived from the original cohort data and all but expectation of life can be used to derive the other functions, it is often inferred that no single function has precedent. Although this is true algebraically, it is not accurate biologically, demographically, or actuarially. The age-specific mortality schedule—the series of probabilities that an individual alive at age x dies prior to age x+1—serves as the actuarial foundation for all other functions.

Why mortality is fundamental:

  1. Death is an "event" indicating a change of state from living to dead; a failure of the system. In contrast, survival is a "non-event" inasmuch as it is a continuation of the current state. This orientation toward events rather than non-events is fundamental to the analysis of risk and hazard rates.
  2. An individual can die due to a number of causes such as due to an accident or to disease. Therefore mortality rates can be disaggregated by cause of death thus shedding light into the biology, ecology, and epidemiology of deaths, the frequency distribution of causes, and the likelihood of dying of a particular cause by age and sex. This concept of "cause" obviously does not apply to survival.
  3. The value of mortality rate at a specified age is independent of demographic events at other ages. In contrast, cohort survival rate (lx) to older ages is condition upon survival to each of the previous ages, life expectancy at age x (ex) is a summary measure of the consequences of death rates over all ages greater than x, and the fraction of all deaths (dx)that occur at young ages will determine how many individuals remain to die at older ages. This independence of mortality rate relative to events at other ages is important because age-specific rates can be directly compared among ages or between populations which, in turn, may shed light on differences in relative age-specific frailty or robustness.
  4. A number of different mathematical models of mortality have been developed which provide simple and concise means for expressing the actuarial properties of cohorts with a few parameters. Therefore the mortality and longevity experience of different populations can be more readily compared.

The Gompertz Mortality "Law"

One of the most fundamental and important parameters in demography, gerontology and actuarial studies is the rate of change or slope of the age-specific mortality schedule with age. In 1825 the English actuary Benjamin Gompertz observed that "the number of living corresponding to ages increasing in arithmetical progression, decreased in geometrical progression." He proposed that a geometrical decrease in survival with age existed because of a geometric increase in the "force of mortality" with age. The Gompertz model has been the major mortality rate model in gerontology for more than 60 years. It is of the form:

x = aebx
(5)

where x is the mortality at age x, a is the initial mortality rate and b is the Gompertz parameter which denotes the exponential rate of change in mortality with age. The Gompertz model is important because:

  1. It defines the concept of an initial mortality rate, q0, which characterizes differences in the overall level of mortality between two populations or cohorts.
  2. It defines the rate of change in mortality with age, G, the Gompertz parameter. This parameter is important because it charactereizes differences in the aging rate of two populations.
  3. The model requires an understanding and designation of the onset of senescence; that is, the age when the exponential rate of aging starts.

The Gender Gap

While women generally outlive men by a margin of 4 to 10 years throughout the industrialized world a long standing question in biology is whether this female advantage in longevity is a general characteristic of most nonhuman species as well. The scientific literature contains conflicting views.

Supportive Views: Hazzard (1990) states "The greater longevity of females than males appears to have a fundamental biological basis. Studies of comparative zoology suggest that greater female longevity is virtually universal". Hamilton and Mestler (1969) begin their paper with the statement, "Males tend to die at an earlier age than females in most species of animals for which data are available". Brody and Brock (1985) state, "...there are basic and fundamental questions posed by the fact that female survival [advantage] seems to be one of the most pervasive findings within the animal kingdom."

Conflicting Views: The paper by Lints and co-workers (Lints et al. 1983) made 218 comparisons between female and male life span in Drosophila melanogaster and concluded that mean life span of females exceeds that of males in only about half the cases. Smith (1989) notes, "...while there is some evidence that adult populations of many animal species contain more females than males, most of these studies do not consider survival to an age approaching the potential limit for the species as implied by the word longevity." Gavrilov and Gavrilova (1991) state "The hopes connected with the search for general biological mechanisms underlying these [sex] differences seem to be in vain, since, despite the wide-spread opinion to the contrary, the greater life span of females is not in itself a general biological regularity".

In 1900 the life expectancy at birth of U.S. women was around 49 years and for men around 47 years--a 2 gap referred to as the gender gap. Mortality rates have decreased over the past 90 years although the rate of decrease for females has been greater than that for males so that currently the gender gap is 7 years--females have a life expectancy of 79 years while for males life expectancy is 72 years.

General determinants of sex mortality differentials:

  1. Constitutional endowment which includes all structural, physiological, endocrinological and immunological factors affecting the ability of individuals of each sex to resist disease, stress, physical challenge and deterioration. This category is concerned with overall "fitness" and includes the direct and indirect effects of chromosomal differences between males and females.
  2. Reproductive biology including the effects of male and female hormones, gonadal development and production of eggs or offspring. This group of factors is concerned with processes typically classified as costs of reproduction.
  3. Behavioral predispositions. These include behavioral traits evolved to maintain territories as well as the "high risk-high stakes" strategy of males of many species for locating, competing for and defending mates.

Donner Party Mortality
(1846-1847)
Out of 90 individuals in the Donner party 32-of-55 males or 58% died whereas 10-of-32 females or 29% of females died. Source: S. McCurdy, Western J. Medicine 160, 338-342 (1994)
Factors interact within and between categories. For example, gender-related exposure to parasites will be affected by differences in male and female behaviors. Once infected the immunological response (endowment) of each sex will modulate survival of parasites which, in turn, is influenced to a large degree by sex hormones. The interaction of the three sex-specific factors--endowment, reproductive biology and behavior--determine the overall susceptibility to death for each sex which, when filtered through environmental, biological and other factors, produce a probability of death. The two concepts--susceptibility and probability--are not equivalent. This is because mortality often runs counter to constitutional frailty due to behavioral factors. Boys die of accidents more frequently than girls, not because boys are more frail but because they take greater risks; reproducing females often experience higher death rates than males of the same age due to the high cost of offspring production and not due to differences in frailty, per se. In both cases, however, the sex differentials in risk-taking or in costs often diminish with age. Consequently differences in frailty or endowment may account for most of the sex mortality differential at older ages whereas differences in both behavior and reproductive biology between the sexes may account for the largest proportion of the sex mortality differential at younger ages, ceteris paribus.

Mortality Crossovers

Mortality crossover--an attribute of the relative change and level of age-specific mortality rates in two population groups: one group is advantaged (lower relative mortality) and the other disadvantaged (higher relative mortality). The disadvantaged population must manifest age-specific mortality rates markedly higher than the advantaged population through middle age at which time the rates change.

Two examples of mortality crossovers

  1. Male-female mortality crossover. In underdeveloped countries as well as in developed countries 50 or more years ago, females experienced higher mortality rates than males from birth through most of their reproductive ages (around 40 years) at which time a mortality crossover occurred. That is, male mortality became higher than female mortality from age 40 through the oldest ages.
  2. Black-white crossover. In this case blacks experience higher mortality rates than white up until age 75 or so at which time the rates crossover and whites experience higher mortality rates than blacks. A fundamental question is both cases is whether the crossover is an artifact of demographic selection--the frail die earlier than the more robust thus leaving only the most robust with lower mortality rates at the older ages. Or whether there are fundamental differences in biology at the level of the individual that account for the crossovers.

Elimination of Mortality

The table below shows how much will life expectancy change if eliminated mortality to various ages from 0 (no elimination) to age 80 years. The point here is that life expectancy at birth will change very little if we eliminate all mortality at early ages or even late ages. Individuals who all live to age 80 are then subject to the mortality experience of all 80 year olds and, on average, would only live 6.2 more years. There are very few 'person-years' to be gained from eliminating more death from younger ages.

Table 1. Effect on expectation of life if mortality up to different ages was completely eliminated.

Age ex Change
0 79.9 .0
20 80.1 .2
40 80.5 .6
60 81.6 1.7
80 86.1 6.2

Cause of Death

Deaths are typically grouped into manner of death, types of causes and classification of main cause. The manner of death refers to natural, accident, suicide or homicide. Four types of causes are commonly recognized:

For example, a person who has diabetes his entire life may be diagnosed with inoperable lung cancer 14 months before his death, with pneumonia 10 days before death and septicemia 2 days before death. Thus septicemia would be the immediate cause, pneumonia an intervening cause, lung cancer the underlying cause and diabetics as a contributory cause.

The underlying cause is the cause used for statistical reporting and is defined as "i)the disease or injury which initiated the train of morbid events leading directly to death; or ii)the circumstances of the accident or violence which produced the fatal injury".

Cause of Death

Persons involved in a death: i)Attending Physician--usually pronounces dead; ii)medical examiner--M.D. who is trained clinician; iii)coroner--usually political appointee; used when suspicious circumstances or homicide, suicide etc. iv)forensic pathologist--M.D. who specializes in pathologies associated with morbidity and death.

Example: i)26% or about 1 out of 4 deaths there was not sufficient cause of death; ii)the autopsy for 88 year old male with Alzheimer's disease provides no clear answers to cause of death.

Example 1:
Ia. Coronary embolism
b. Arteriosclerotic heart disease*
c. Influenza
Example 2:
Ia. Oesophageal varices & congestive heart failure
b. Cirrhosis of liver* and chronic rheumatic heart disease

* denotes the underlying cause of death

Table 2. Autopsy findings in an 88 year old male with Alzheimer's disease (from Martin 1988).

  1. Alzheimer's disease with extensive involvement of hippocampus and neocortex
  2. Bilateral patchy bronchopneumonia
  3. Congestive heart failure
  4. Atherosclerosis
  5. Poorly differentiated prostate adenocarcinoma

ADDITIONAL READING

Chiang, C. 1984. The Life Table and its Application. Robert E. Krieger Publishing Co., Malabar, Florida.

McCurdy, S. A. 1994. Epidemiology of disaster. the Donner party (1846-1847). Western Journal of Medicine 160:338-342.

Moriyama, I. M. 1956. Development of the present concept of cause of death. Amer. J. Public Health 46:436-441.

Return to the Course Syllabus